Em Machine Learning os parâmetros dos modelos são variáveis que são ajustadas durante o treino. Parâmetros também podem ser chamados de coeficientes ou pesos.
Para o modelo de Regressão Linear temos os parâmetros w e b. O parâmetro b pode ser chamado de intercept. Dependendo dos valores desses parâmetros as linhas retas podem ser diferentes .
Veja alguns exemplos de diferentes valores para w e b.
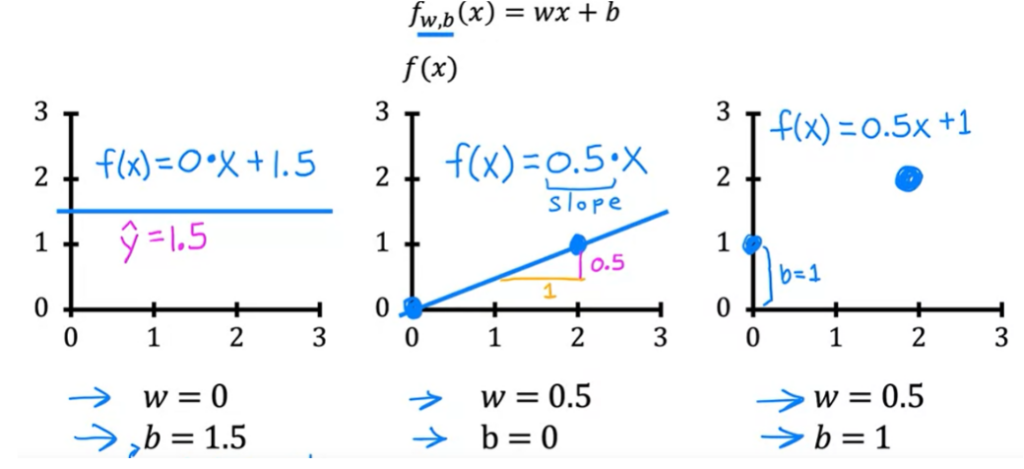
Mas como encontrar os melhores valores para w e b ?
Lembrando que y são os valores reais, e y^ são os valores previstos pelo modelo. Para encontrar w , b que melhor se ajustam o modelo, consiste em ter os valores de y^ mais próximos de y, para todos os dados do conjunto de treino.
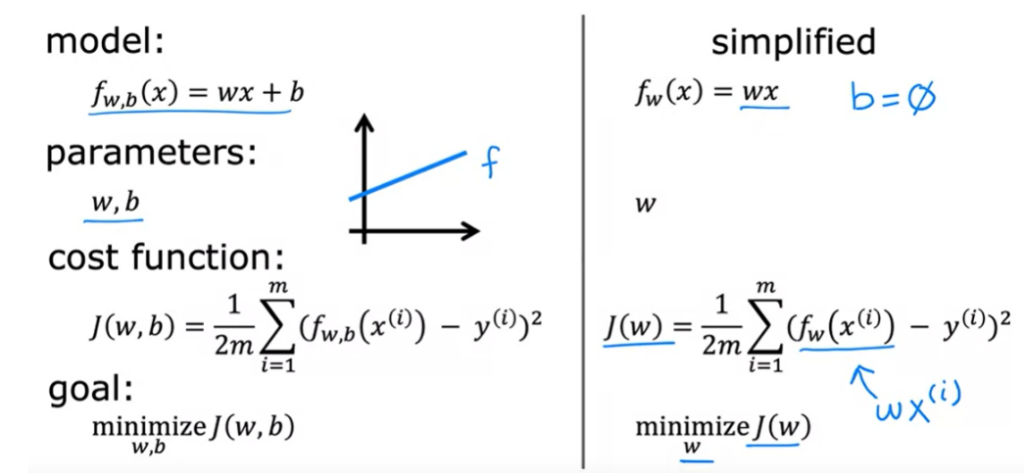
O principal objetivo é ajustar uma linha reta ao conjunto de dados de treino. Mas também precisamos medir quão bem essa linha se ajusta aos dados. E para isso contruimos a função de custo.
Função de Custo ( J )
Função que calcula a diferença entre y^ e y, ou seja mede o quão distante a previsão está do valor real. Essa diferença é chamada de erro (error).

Para calcular a função:
- Calcula a diferença de y^ e y , para cada instância.
- Calcula o quadrado de cada diferença.
- Soma todas as diferenças ao quadrado.
- Divide pelo número de instâncias.
Squared error é comumente usado para regressao linear.
Queremos minimizar J em função de f (w,b).
Pontos Importantes a se observar:
- O valor de y depende do valor de x.
- W controla a inclinação da linha reta.
- J depende do parametro W.
Exemplos
- Se W = 1, a inclinação da reta é 1. E o custo é 0.
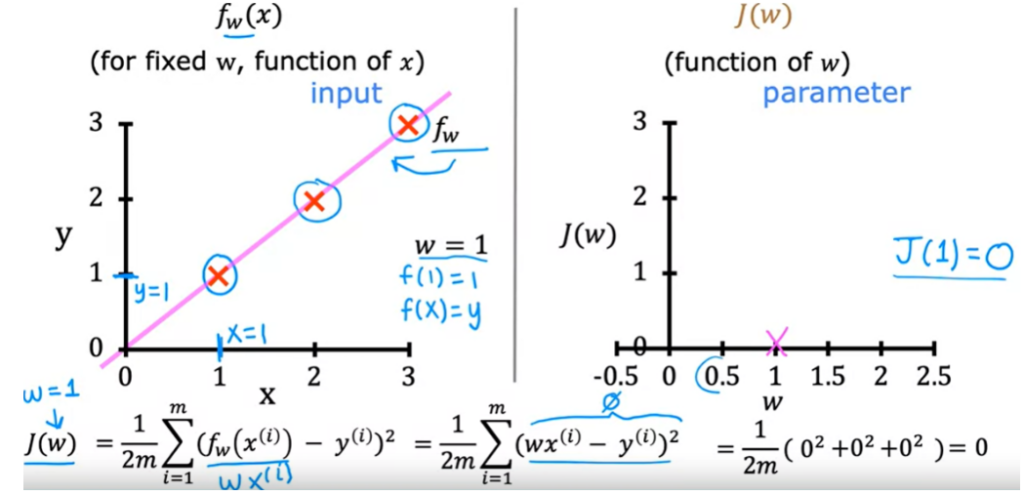
2. Se W = 0.5, a inclinação da reta é 0.5. E o custo é 0.
3. Se W = 1 , f(x) = 0.5, o custo é (0.5 – 1) ² , mas a função de custo é a soma de todas as diferencas.
quando x = 2, f(x) = 1 , e o valor real é 2, entao a função de custo é (1-2)² .
quando x = 3, f(x) = 1 , e o valor real é 3, entao a função de custo é (1-3)² .
A soma de todos = 3.5
m é 3, pois tem 3 pontos de dados
1/(2*3) * 3.5 = 0.58
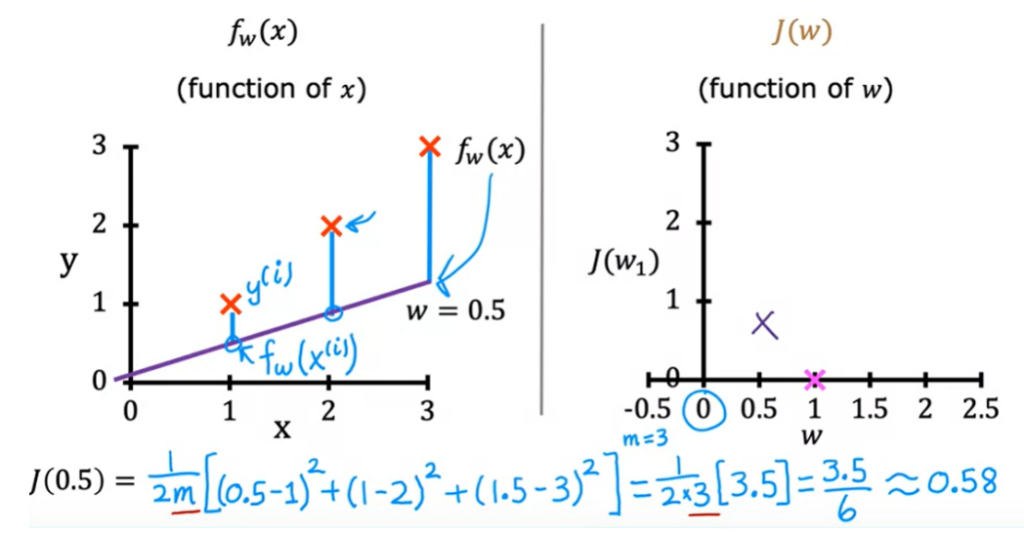
O erro será a distancia entre o dado real e o previsto por f. O erro é a altura da linha vertical.
Se w for negativo, a inclinação da reta será inversa, para baixo. o que gera um custo alto 5.25
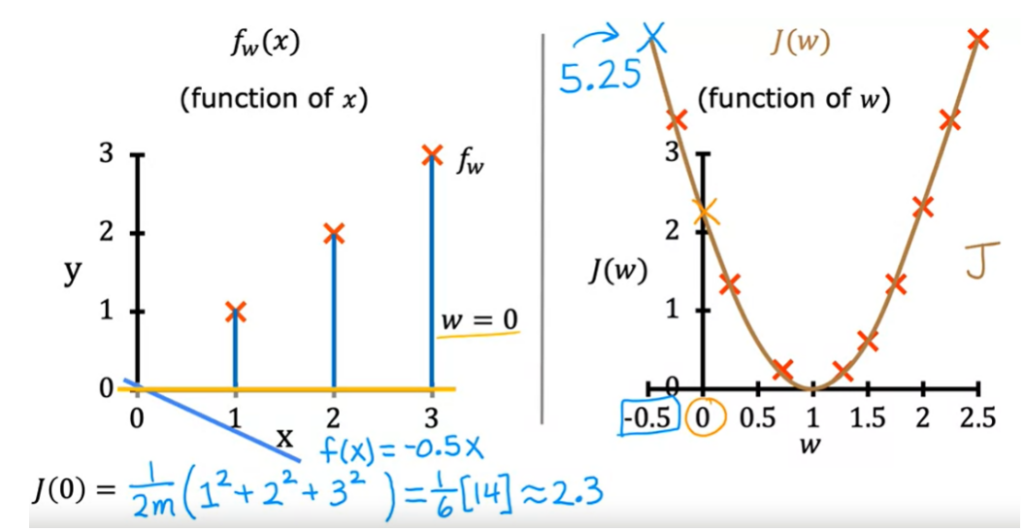
Como escolher o valor de J onde f(x) esteja melhor ajustada aos dados?
Precisamos escolher o valor de W que gera o menor valor em J(w).
J é a função de custo que mede quão grande são os erros ao quadrado, então escolhendo W que minimize esses erros, geramos uma menor valor, e portanto um melhor modelo.
No exemplo, escolhemos o menor valor de J, que é 0 quando o W = 1
Quando o custo é pequeno, próximo de zero, significa que o modelo se ajustou bem aos dados comparando as escolhas de W e b.
Exemplo: Temos o conjunto de dados de treino de preços e tamanhos das casas. Vamos escolher uma função. Se olharmos o gráfico a direita vemos que não é uma boa função. Vemos que nenhum dado foi ajustado a reta. Os preços são subestimados.
Quando temos apenas o parametro w, a função de custo tem o formato de uma parabola
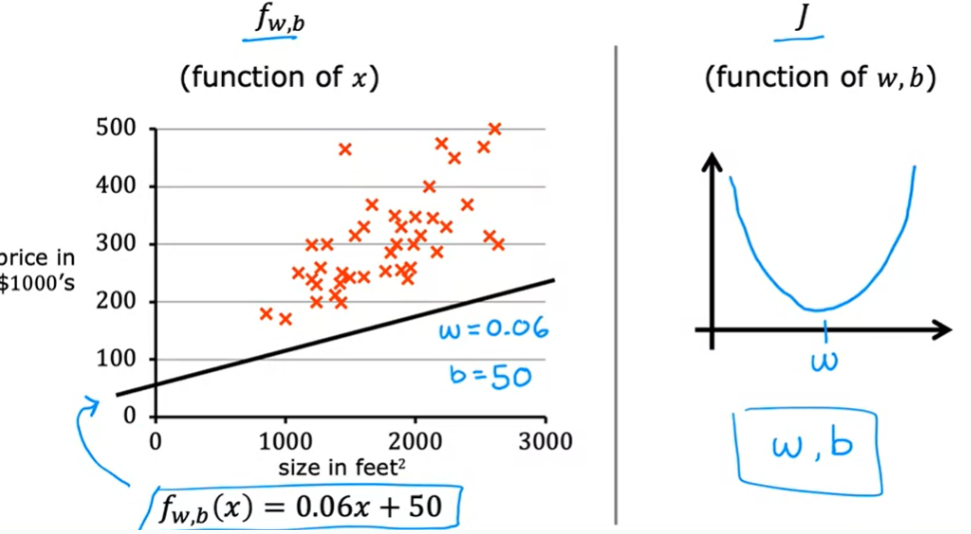
Vizualização de parâmetros
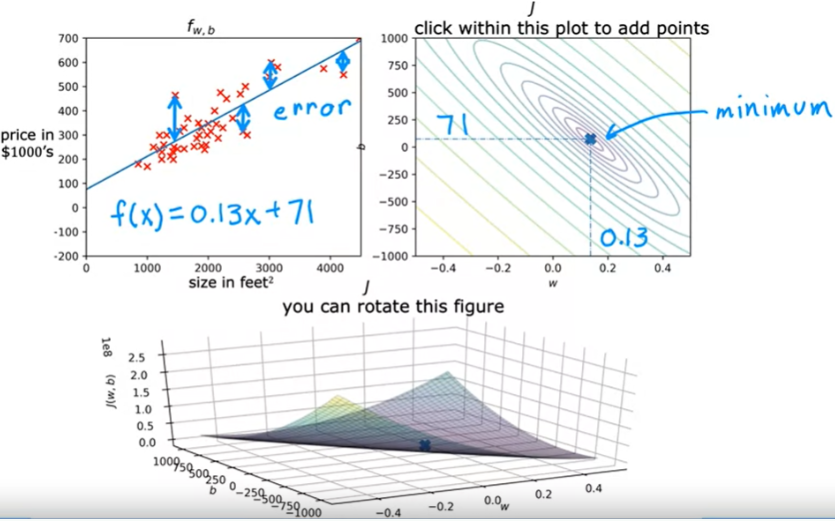
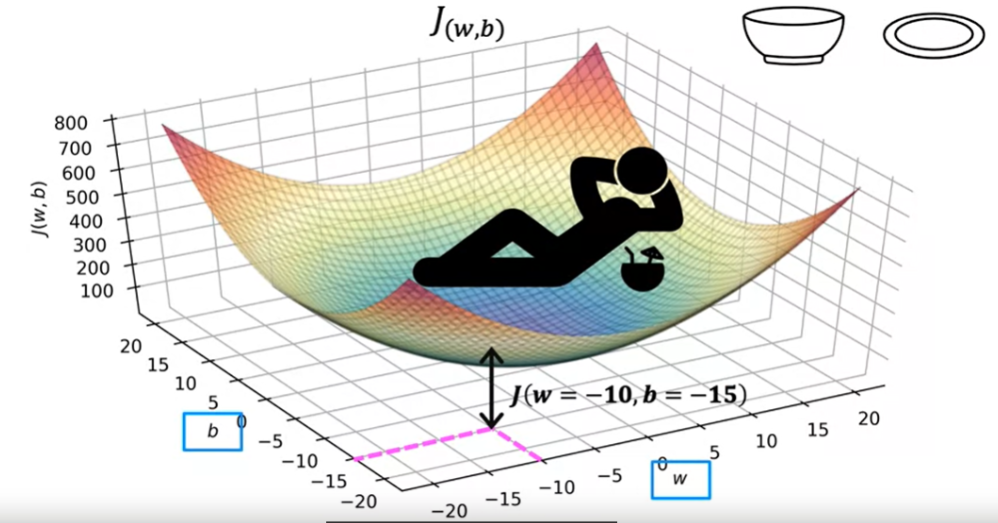
Quando temos o parametro W e b, a visualização se torna mais complexa, a função de custo passa a ter três dimensões, conforme imagem abaixo.
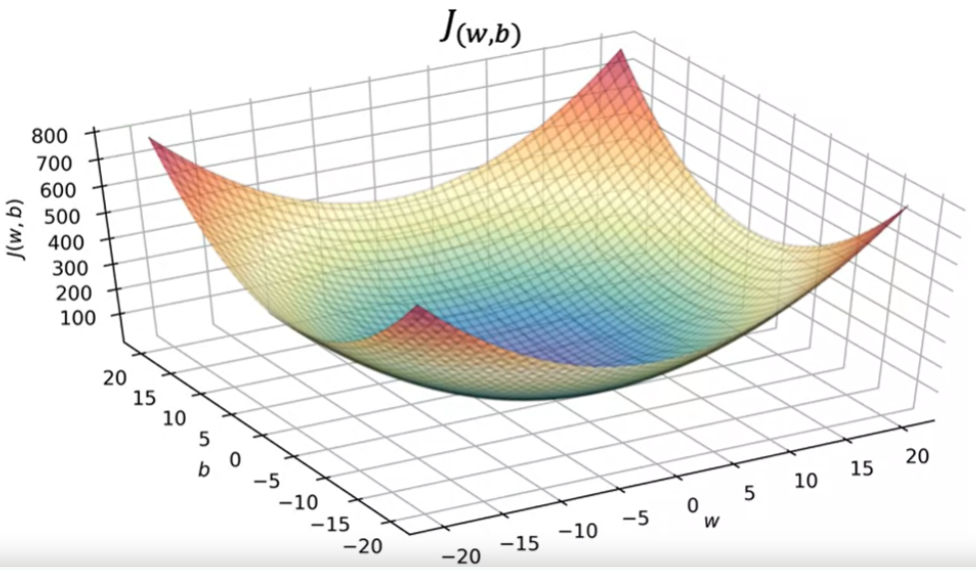
Para w =-10 e b = -15, a altura da superficie sobre o ponto é o valor J.
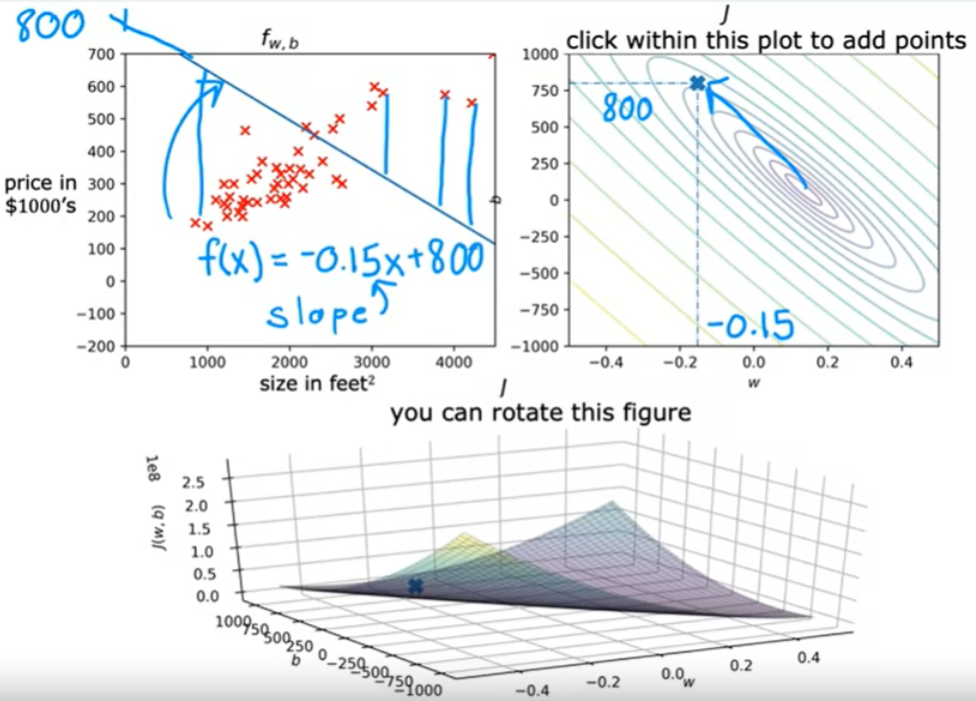
O exemplo abaixo mostra que W e b não se ajustam bem aos dados de treino. No gráfico de custo J, podemos ver que o valor de 800 está distante da posição mínima.
O exemplo abaixo também mostra um grafico onde a função não se ajusta bem aos dados, o valor de b está distante do valor minimo na função de custo.
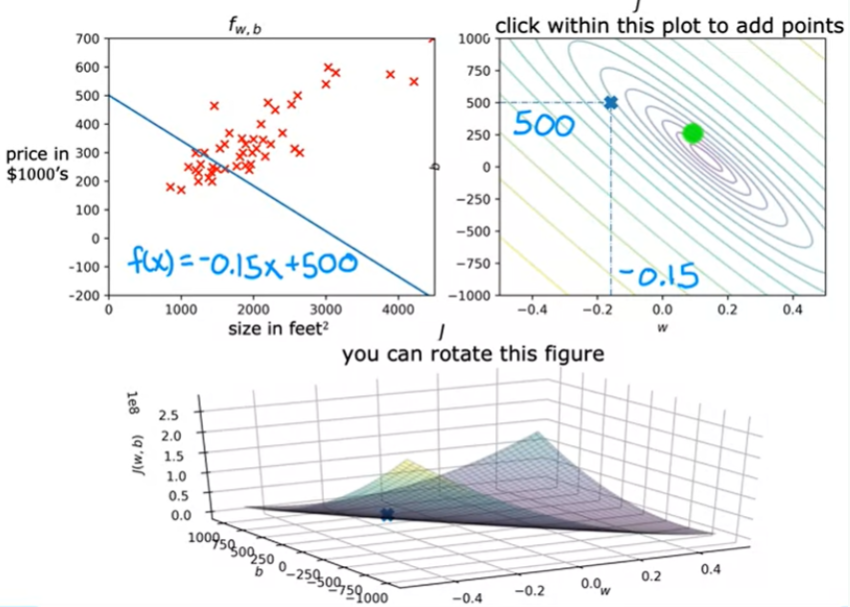
O exemplo abaixo mostra uma boa escolha dos parâmetros onde o ponto que representa o custo está bem próximo do ponto mínimo , não é exatamente o mínimo mas está bem próximo. Assim como a soma dos valores de erros quadrado é a mínima possível.